 |
Maxwell View and Maxwell's Optical Theorems | Maxwell Legacy Concepts |
|---|
In a nutshell |
Maxwell was interested in optical phenomena throughout his life, including boyhood exploration and investigations while he lived at Glenlair. These developed into detailed and innovative work on polarisation, colour and, in his 20s, on optical instruments. One of the most innovative instruments of the 1850s was his ‘colour box’, for quantitative experiments on colour matching using selected colours from a spectrum. Without even drawing the reader’s attention to it, the colour box incorporated a new configuration of lens-work now known as the 'Maxwell view’. Some technical detail of this is given below. Also, while professor at Aberdeen Maxwell developed a project he had begun at Cambridge, namely to look at the general conditions for forming images in optical instruments and draw out general conclusions. The result were a number of ‘optical theorems’, all of which are still valid and some still explicitly useful. More technical detail can be found below. |
 |
|---|
| Technical detail | Maxwell view: The Maxwell view is a technique in optical instrument design that is elegant, simple and effective. Maxwell devised it for creating the appearance of uniform illumination. The diagram above shows the idea reduced to its simplest. There is no eyepiece in this arrangement. The observer’s eye is placed beside an open hole; the image of a source that may be irregular is formed at the pupil of the eye (not the back of the eye). If the image of the source is smaller than the pupil then all light from the source enters the eye and what is seen is the outline of the lens uniformly illuminated even if the source itself is irregular. 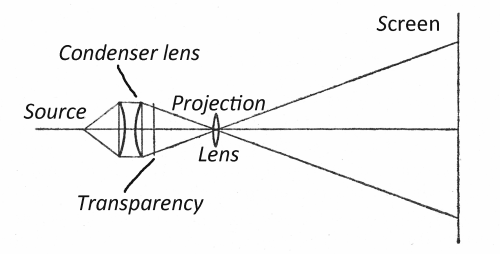
Imaging of the source of light in a typical projector to obtain uniform illumination on the screen using the Maxwell view idea.
The Maxwell view has entered optical design in other circumstances, so much so that Maxwell is rarely singled out as its originator. Uniform illumination over a wide area such as a screen can be arranged by having a wide source or a diffuser, like frosted glass. Both these systems tend to waste a lot of light. The slide projector, the overhead projector and the traditional film projector all have the problem that they get the maximum amount of light into a greatly magnified image by having a small, bright source but the irregularity of the light source readily appears on the screen unless care is taken. The Maxwell view technique is applied here to focus the source onto the projection lens using a ‘condenser lens’ (strictly, the entrance pupil of the projection lens for a compound lens). In this case, no image of the source can appear on the screen and all the light collected by the condenser reaches the screen. [The condenser lens is frequently a pair of large diameter plano-convex lenses, cheap to make but reducing spherical aberration of the source so that it is imaged satisfactorily]. In effect there are two separate but interleaved image-forming systems, one for the light source and one for the object being projected. Maxwell's optical theorems: Maxwell’s optical theorems embrace several results he deduced in 1856/7 exploring the theoretical limits of perfect imaging. Maxwell picked up on the work of Gauss ‘who treated the subject with that combination of analytical skill and practical ability which he displays elsewhere’. Gauss had deduced that any optical system can be characterised by a small number of parameters (the cardinal points). This allowed Maxwell to ignore the disposition of lenses and mirrors in any particular system and look at an optical instrument in general as a device that mapped object points into image points (Maxwell's 'collinear transformations'). Maxwell defined what he meant by a perfect imaging system and went on to prove 9 ‘propositions’. Two are singled out below as ones that turn up in optics textbooks.
References: James Clerk Maxwell On the General Laws of Optical Instruments, Quart. J. of Pure & Appl. Math., February 1858, II, 233-246. The Maxwell view is discussed at fuller length in R. S. Longhurst, Geometrical and Physical Optics, [Longman, London, 3rd ed'n 1973]. JSR 2016 |
|---|