 |
Maxwell-Boltzmann Statistics | Maxwell Legacy Concepts |
|---|
In a nutshell |
Maxwell-Boltzmann statistics introduced an idea at the heart of modern physics. The ‘statistics’ refers to the probability that a given configuration in a complicated system will occur. The configurations relate to the number of ways a system can be arranged with a particular property. The idea is applied to explain why the second law of thermodynamics comes about when a system is composed of a very large number of small components. The original application considered a gas composed of a huge number of molecules. In general there are vastly more configurations that have the components more or less randomly distributed than there are ordered configurations. If all configurations are equally likely then a random configuration is favoured over an orderly one. Any change is therefore likely to increase the randomness of the components. Maxwell realised in the 1860s that probability was at the heart of how a system developed over time and that the idea that future behaviour was fully determined was incorrect when the information one has about a system is necessarily statistical. The future may be more disordered than the past but, he pointed out, it was intrinsically more predictable than the past. This was about half a century before probability was shown to be a central concept in our understanding of the quantum world. An informal analogy that conveys something of the idea is that if a room starts tidy and to someone looking in to the room the objects appear to get moved around almost at random over time, then the room inevitably gets more chaotic, for there are far more chaotic arrangments than there are tidy arrangements. The chances of almost random motion producing tidiness is negligible. Of course this isn't a precise analogy, for objects in a room are moved by intelligence and intelligence can create order in limited circumstances. Also the room and objects aren't 'isolated', which is one of the conditions needed, as discussed below. Maxwell-Boltzmann statistics enables the distribution of particles over their possible range of energies to be found as one that exponentially decays with incresing energy. This is discussed more fully below. |
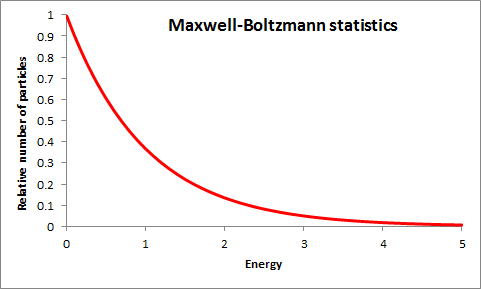
Maxwell-Boltzmann statistics predicts that the probability of a particle having larger energy decreases exponentially
|
|---|
| Technical detail | Maxwell-Boltzmann statistics come about through looking at the possible states of a system at its atomic or molecular level. Nowadays this is in fact easier than in Maxwell and Boltzmann's day, for states are a key way of describing atoms and molecules in quantum mechanics. Maxwell and Boltzmann were particularly concerned with the properties of gases. A 'box' containing the gas was mentally divided into a very large number of tiny rectangular cells in 3 directions x,y,z. A molecule not only has position but also has momentum components px,py,pz that can be considered in momentum cells. This introduces the idea of 'phase space', which is the space of position and momentum of each particle. For each particle, phase space has 6 components. The 'microstate' of the system is the set of occupied cells in phase space of all the particles. Maxwell-Boltzmann statistics lets you calculate how these states are occupied. Think about the behaviour of a gas in an isolated container. As the gas molecules move around and collide the set of microstates of the system rapidly change. The total energy of an isolated system must remain constant so not all possible microstates (i.e all possible combinations of position and momentum of the components) will occur. A key assumption by Maxwell is that all microstates of a given energy are equally likely. In textbooks the microstates may be called degrees of freedom and the assumption denoted the equipartition of energy among the degrees of freedom . The energy of the individual components will vary, though. Maxwell-Boltzmann statistics is the mathematical expression used to find how the energy of the components is spread in these, and analogous, circumstances. What has this to do with 'luck', which seems to be illustrated by the dice? The dice for the moment represent molecules, the number showing on a face represents the energy of a molecule. For simplicity there are only 10 molecules in the picture each with 6 possible energies in our isolated system. As the molecules collide with each other their energies constantly change. Their 'state' at one time is represented by a throw of the 10 dice. There are a vast number of possible states (610= 60466176) but most of them are not 'allowed' because one condition of an isolated system is that its energy is constant. The only allowed states will be those that all have the same total energy. The total energy is the sum of the faces showing on the 10 dice. Let's choose 20 as a representative sum. There are 85228 ways the 10 dice can add up to 20. Believe me, I've counted. Out of the 10 dice, up to 8 could be 1s but no more than 2 could be 6s so clearly there are more 1s than 6s among these 85228 selections. Counting again, which is where the 'statistics' comes in, 1s occur 393030 times and 6s only 12870. The histogram below shows the relative numbers, labelled as the frequency at which a given face shows. This is analogous to Maxwell-Boltzmann statistics, with an almost exponential fall-off of populated states with increasing energy. 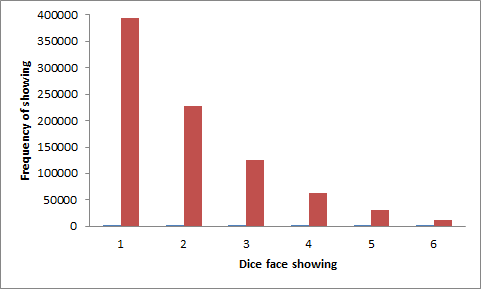
Energy distribution created by the dice simulation showing the number of faces with a given number of spots (the energy) in all possible combinations of 10 dice that add up to 20. See text! The fun with the dice (well, I enjoyed the counting) shows nicely how energy can be distributed but it gives an incomplete picture of the message of Maxwell-Boltzmann statistics. A central issue is how microstates are distributed in phase space, in particular that the equilibrium configuration will fluctuate around the most probable distributions. All other distributions, even those with the right energy, are unlikely to occur because there are so many more distributions close to the most probable ones. This isn't obvious with a small number of particles but in a thimblefull of atmosphere there are over 1019 molecules and then it is very true. Suppose the dice are re-interpreted to represent the number of molecules in a given cell in phase space. Each spot on a dice now represents a molecule. The total number of molecules is constant and hence (as before) the changes taking place with time must preserve the sum of the spots. In Maxwell-Boltzmann statistics all the particles are distinguishable and hence we have to count the spots as distinguishable, say of they are of different colours1. It was Boltzmann who showed that the probability of a configuration was proportional to the sum of the logarithms of the occupation numbers of each cell (i.e. the numbers showing on the dice). This is identified as a measure of the entropy of the system. A gas not in equilibrium will evolve to maximise its entropy just because this represents the maximum probability among the possible states of its constituents. The motivation for both Maxwell and Boltzmann was to understand gases but it later became apparent that their ideas were very widely applicable. Imagine that a gas is let into an almost empty chamber through a nozzle at one side. It will quickly spread out towards the most probable distribution, which is one uniformly filling the chamber. On a slower timescale, think of a drop of ink allowed to fall into a beaker of water. Much more slowly than a gas moves, the ink will diffuse throughout the beaker to take up its equilibrium configuration. If you could collect statistics on the location and speed of ink molecules in the water you would be able to predict that in future the odds of the ink congregating in one part of the beaker are almost infinitesimally small. The ink will stay diffused throughout the beaker. Seeing the ink all through the beaker, you could not deduce that at some time in the past the ink was altogether in one small drop just below the surface and even if you thought it might have been you can't deduce how long in the past that was. This is what Maxwell meant by saying that the future distribution of matter in motion is more predictable than its past history. Returning to the dice representing energies, of course 6 available energies is a gross simplification. Moreover, in the realm of discrete energies and atomic or molecular objects quantum mechanics rules. One important difference is that in quantum mechanics, particles of the same kind are indistinguishable. The main reason for the large number of possibilities in arranging the dice in the previous example is that every die in the row has been taken as distinguishable from every other one. For example, there are 10!/(4!4!) (= 6300) ways of rearranging the same set of dice as are illustrated. In quantum mechanics that arrangement would be counted only once. Quantum particles obey either Fermi-Dirac or Bose-Einstein statistics. In spite of the apparent gross overcounting, Maxwell-Boltzmann statistics are a good approximation in many circumstances even though they don't strictly apply at an atomic level. That was found out in the 20th century, long after either Maxwell's or Boltzmann's time. 1footnote: This footnote might help in understanding the reason why a large number of cells concentrates the system near the most likely configuration. Suppose there are N = 1019 cells in a small volume containing 2×1019 molecules. The microstate that has the most number of possibilities of occurring is the one where the molecules are uniformly distributed throughout the volume, i.e. there are 2 molecules in each cell. The number of possibilities P is N!/2!N. Call this P. Now suppose just 1% of the cells change to an occupation of 3 and 1% to an occupation of 1 (to preserve the total number of molecules). The number of possible microstates is now N!/(2!0.98N*3!0.01N*1!0.01N). Call this P’. The ratio of P’/P after a couple of lines = (2/3)0.01N = e0.01N*ln(2/3) ≈ e-0.004N. Given that N = 1019, the ratio of P’/P is incredibly small so even this minor fluctuation from equilibrium is really unlikely to happen, for the number of microstates available with this slightly non-uniform distribution is comparatively tiny. There is one redeeming feature in that the mean time between molecular collisions under normal atmospheric conditions is around 10-10 seconds so the 1019 dice are thrown about this often. In 1860 Maxwell introduced the concept of the number of collisions per second experienced by a typical molecule and found it was about 1010. He was ‘in the right ball-park’. Even a 1-in-a-billion fluctuation from the mean will very fleetingly occur a few times a second, meaning that the density in every small volume of the gas fluctuates. This phenomenon is responsible for the twinkling of stars and, more subtly, for the blue colour of a clear sky. JSR 2016 |
|---|